Sommaire
Généralités
Limites
Lien avec la fonction exponentielle
Dérivée
Intégrale
Exercices
Intérêt de la fonction ln
Nous allons voir dans ce cours une fonction importante : la fonction ln.
On note ln(x) et on prononce « hélène de x », comme le prénom !
Commençons par tracer la courbe de la fonction :
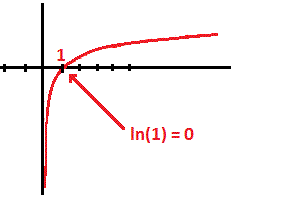
A partir de la courbe on peut voir pas mal de choses intéressantes.
Tout d’abord, on voit que la fonction n’est définie que sur ]0 ; +∞ [ !!
Donc ln(-4) n’existe pas ! Mais ln(5) existe.
Ensuite, au niveau du signe de la fonction, on voit qu’elle est négative jusqu’à 1, puis postive, donc
\(\displaystyle ln(x) < 0 \, sur \, ]0 ; 1[ \)
\(\displaystyle ln(x) \gt 0 \, sur \, ]1 ; + \infty \)
Et en 1 ? Et bien ça vaut 0 :
\(\displaystyle ln(1) = 0 \)
—
Attention ! Beaucoup d’élèves disent ln(0) = 1, ce qui est archi-faux !
Ils confondent avec la fonction exponentielle, où là oui e0 = 1, mais pour la fonction ln c’est l’inverse, c’est ln(1) = 0 
—
Par ailleurs, la fonction ln est STRICTEMENT CROISSANTE. On va également s’en servir par la suite.
La fonction ln a également d’autres propriétés à connaître : pour x et y strictement positifs :
\(\displaystyle ln(x \times y) = ln(x) + ln(y) \)
\(\displaystyle ln(\frac{x}{y}) = ln(x) – ln(y) \)
\(\displaystyle ln(\frac{1}{x}) = -ln(x) \)
\(\displaystyle ln(x^n) = n \times ln(x) \)
Par exemple :
\(\textstyle ln(3x) = ln(3) + ln(x) \)
\(\textstyle ln(5) + ln(6x) = ln(5 \times 6x) = ln(30x) \)
\(\textstyle ln(\frac{3x}{7}) = ln(3x) – ln(7) \)
\(\textstyle ln(8) – ln(4) = ln(\frac{8}{4}) = ln(2) \)
\(\textstyle ln(\frac{1}{5}) = -ln(5) \)
La dernière formule peut-être utile quand on a une équation dont l’inconnue est en exposant :
\(\textstyle 5^x = 12 \)
\(\textstyle ln(5^x) = ln(12) \)
\(\textstyle xln(5) = ln(12) \)
\(\textstyle x = \frac{ln(12)}{ln(5)} \)
Ce genre de cas se retrouve surtout en probabilités, pense donc à utiliser la fonction ln dans les équations (ou même les inéquations) quand l’inconnue est en exposant.
—
ATTENTION ! Les formules ci-dessus ne sont valables que pour x et y strictement positifs !!
En effet, ln(-8 &;times (-3) ) existe par exemple, puisque cela est égal à ln(24).
Mais ln(-8 &;times (-3) ) n’est pas égal à ln(-8) ×, ln(-3), puisque ln(-8) et ln(-3) n’existent pas !!
—
Tu remarqueras que les propriétés ressemblent fortement aux propriétés avec les arguments dans le chapitre des complexes.
Si tu ne l’a pas encore vu ce n’est pas grave, tu le verras plus tard^^.
Parlons limite maintenant !
On voit facilement avec la courbe que :
\(\displaystyle \lim_{x \to 0} ln(x) = -\infty \)
\(\displaystyle \lim_{x \to + \infty} ln(x) = +\infty \)
La seule difficulté ici, c’est quand on a des fonctions composées, mais cela reste assez simple!
Voici quelques exercices sur les limites de fonctions composées pour s’entraîner.
De plus, il faut connaître deux limites particulières :
\(\displaystyle \lim_{x \to 0} x \times ln(x) = 0 \)
\(\displaystyle \lim_{x \to + \infty} \frac{ln(x)}{x} = 0 \)
Normalement ces deux limites sont des formes indéterminées, ce pourquoi il faut les apprendre par coeur. Mais il y a un moyen simple de les retenir : tu fais comme si il n’y avait pas ln(x), mais seulement x !
\(\displaystyle \lim_{x \to 0} x \times ln(x) = \lim_{x \to 0} x = 0 \)
\(\displaystyle \lim_{x \to + \infty} \frac{ln(x)}{x} = \lim_{x \to + \infty} \frac{1}{x} = 0 \)
Cela vient du fait que x » domine » ln(x), c’est-à-dire que ln(x) est négligeable devant x, ce pourquoi on fait comme si il n’y avait pas ln(x).
On retrouve la même propriété pour la fonction exponentielle, sauf que là c’est x qui est négligeable devant ex, donc on fait comme si il n’y avait pas de x.
A noter que ces propriétés sont vraies pour toutes les puissances de x, donc x2, x3, x4, x5…
Exemple :
\(\displaystyle \lim_{x \to 0} x^8 \times ln(x) = 0 \)
\(\displaystyle \lim_{x \to 0} x^{24} \times ln(x) = 0 \)
\(\displaystyle \lim_{x \to + \infty} \frac{ln(x)}{x^{15}} = 0 \)
\(\displaystyle \displaystyle \lim_{x \to + \infty} \frac{ln(x)}{x^6} = 0 \)
Voyons à présent une fonction que l’on trouve souvent avec ln : la fonction exponentielle !
Pour plus de précisions sur cette fonction, va voir le cours sur la fonction exponentielle
Mais quel est le rapport avec exponentielle ?
Et bien tout simplement :
\(\displaystyle e^{ln(x)} = x \)
\(\displaystyle ln(e^x) = x \)
Les deux fonctions » s’annulent » entre elles. C’est ce qu’on appelle des fonctions réciproques.
D’accord c’est bien beau tout ça mais ça sert à quoi ?
A plein de choses !  Notamment à résoudre des équations ou inéquations avec des exponentielles.
Notamment à résoudre des équations ou inéquations avec des exponentielles.
Par exemple, si on veut résoudre :
5 < ex
on applique la fonction ln, et on ne change pas le sens de l’inégalité car la fonction ln est croissante !!!!!
ln(5) < ln(ex)
ln(5) < x
de même, si on a
ln(x) < 9
on applique la fonction exponentielle, et on ne change pas le sens de l’inégalité car la fonction exp est croissante !!!!!
eln(x) < e9
x < e9
—
ATTENTION ! Note bien qu’il faut absolument justifier comme on vient de le faire en disant que la fonction ln ou exponentielle est croissante, il serait bête de perdre des points à cause de ça, surtout que les professeurs adorent quand tu justifies, mais détestent quand tu ne justifies pas 
—
Comme tu le vois, c’est très simple ! Entraîne toi avec ces exercices sur les inéquations
La dérivée de ln n’est malheureusement pas aussi simple que celle de exponentielle, mais elle reste assez facile^^
La dérivée de ln(x) est 1/x :
\(\displaystyle (ln(x))’ = \frac{1}{x} \)
Jusque-là c’est simple, mais il faut faire cependant attention aux fonctions composées !! Si tu n’en t’en souviens plus, va voir le chapitre sur les dérivées composées.
Regardons quelques exemples :
g(x) = ln(x3 – 9x + 4), c’est une fonction composée : ln(u), avec u = x3-9x + 4
La dérivée de ln(u) est u’/u :
\(\displaystyle (ln(u))’ = \frac{u’}{u} \)
Ici comme u = x3 – 9x + 4, u’ = 3x2 – 9, donc
\(\textstyle g'(x) = \frac{3x^2-9}{x^3 – 9x + 4} \)
C’est comme d’habitude, on dérivé normalement et on multiplie par u’ ! Rien de méchant 
Rappelle toi juste que la dérivée de ln(u) est u’/u ! Avec le temps et quelques exerccies sur les dérivées composées ça deviendra tout naturel 
La primitivede ln(x) est xln(x) – x. Cependant, en terminal tu n’as pas à le savoir, nous ne ferons donc pas d’exercices particuliers là-dessus.
En revanche, la fonction ln peut se retrouver dans des intégrales composées !
En effet, d’après le cours sur les intégrales et primitives, on sait que la primitive de u’/u est ln(u) !!
\(\displaystyle \int\limits_a^b \frac{u'(x)}{u(x)}dx= [ln(u)]_a^b = ln(u(b)) – ln(u(a)) \)
Voyons un petit exemple :
\(\displaystyle A = \int\limits_2^3 \frac{2x^3 – 1}{x^4 – 2x + 5} dx \)
Si on pose u = x4 – 2x + 5, on a u’ = 4x3 – 2.
Au numérateur, on a 2x3 – 1, ce n’est donc pas u’, mais ça ressemble beaucoup !
En effet, u’ = 4x3 – 2 = 2 × (2x3 – 1) !!
Ainsi il faudrait faire apparaître un 2 au numérateur.
Comment on fait ? Et bien on multiplie par 2 en haut et en bas !
On a donc
\(\displaystyle A = \int\limits_2^3 \frac{2 \times (2x^3 – 1)}{2 \times (x^4 – 2x + 5)} dx \)
Il n’y a que le 2 du haut qui nous intéresse, pas celui du bas, et comme c’est une constante, on peut le sortir de l’intégrale !
D’où
\(\displaystyle A = \frac{1}{2} \int\limits_2^3 \frac{2 \times (2x^3 – 1)}{x^4 – 2x + 5} dx \)
et là on a bien u’ /u !!
On peut alors utiliser le fait que la primitive de u’/u est ln(u) :
\(\displaystyle A = \frac{1}{2} [ln(u)]_2^3 \)
\(\displaystyle A = \frac{1}{2} [ln(x^4 – 2x + 5)]_2^3 \)
\(\displaystyle A = \frac{1}{2} (ln(3^4 – 2 \times 3 + 5) – ln(2^4 – 2 \times 2 + 5)) \)
\(\displaystyle A = \frac{1}{2} (ln(80) – ln(17)) \)
\(\displaystyle A = \frac{1}{2} \times ln(\frac{80}{17}) \)
car ln(b) – ln(a) = ln(b/a)
—
Attention, ne pas oublier le 1/2 devant l’intégrale !! Il faut sortir les constantes qui ne servent pas à calculer la primitive comme le ½ ici par exemple, mais il ne faut pas oublier de les mettre dans la suite du calcul !!
—
Comme tu as bien appris ta leçon, nou allons te proposer non pas une mais DEUX vidéos 
La première comporte des intégrlaes où ln est la primitive, tandis que dans la deuxième, ln est à la fois dans l’intégrale et dans la primitive.
Nous avons regroupé ces 2 vidéos sur la même page, donc n’oublie pas qu’il y a une autre vidéo en-dessous de la deuxième 
Tu trouveras sur cette page tous les exercices sur la fonction ln !
Bon et bien voilà, c’est tout ce que tu as à savoir sur la fonction ln ! Il faut surtout retenir ses propriétés avec les calculs, car on retrouve souvent cette fonction dans les intégrales, les études de fonctions, les exercices avec exponentielle…
Le principal intéret de la fonction ln est d’être la fonction récipropque de exponentielle, qui est une fonction fondamentale, surtout en physique ! Tu es donc susceptible de la rencontrer souvent^^
Retour au sommaire des coursRemonter en haut de la page

Super! Je parcourais désespérément le net afin de trouver un cours simple afin de m’aider à réaliser mon Devoir maison (Bon pour le devoir cela ne m’a pas totalement aidée) , et je trouve vos cours vraiment géniaux ! Avec tous ses petits conseils en or, merci ! 🙂
j’espère que c’est vous qui pouvez nous satisfaire nous les élèves intélligents, pas vous, en aucun cas.merci !!!
je suis vraiment content pour la bonne comprehension pour ces proprietes et des seris d’exercices
Super grâce aux différentes cour sur ln et aux méthodes je vais pouvoir me préparé pour la classe de terminale merci beaucoup
j’adore les cours de math mais je n’ai jamais compris les primitives , integrales alors je demande votre aide
merci de votre pertinence d’information. Je crois que vos conseils nous aiderons a mieux afronté les exercices de mathematiques. Merci
super , simple et efficace ,
quelques cas complexes seraient très bien , merci
Avec cette méthode géniale les élèves vont apprécier les maths.
Supeeeer je suis très content parce-que j’ai compris Ln merci pour la bonne présentation
avec ça, mon bac est assuré. merci infiniment.
J’adore cette cours..
Super je suis très content parceque j’ai compris Ln merci pour la bonne présentation
Il manque ln(racine de x ou de u(x))
Sinon cours tres bien expliqué.
Génial et vraiment merci pour vos cours
C’est bien de votre manière sinon je n’avais rien compris sur la leçon
Je vois mieux maintenant…..
C’est très bon , ça plus . cela me permettra de réviser sans mon cahier pour l’Université
Waouh c’est bizarre. Je comprends mieux. Merci pour tout.
MERCI
merci d’avoir l’aider
Les cours sont géniaux !
Cool votre site
Franchement merci pour ces bons conseils il y a certaines choses que je n’avais pas compris pendant toute l’année de terminale et maintenant je suis éclairé donc merci beaucoup pour ces précisions qui vont m’apporter beaucoup pour mon bac 2017 Merci
Ce cours m’a beaucoup aidé. merci!!!
Waouuh merci beaucoup
C’est incroyable comment les maths peuvent devenir facile d’un prof à un autre. Merci, vous faciliter des choses que les gens expliquent avec tant de peines.
Je vous Remercie Beaucoup Ce Site Est Super Cool
methodemath c’est tres important
on sais pas comment vous remercier
salut. mes respects pou celui ou ceux qui ont elaboré cette enorme et exelente explication. sa facilite beaucoup l’aquisition du cours . je suis tres chanceux de trouver ce site il me sert pour faire des revisions pour aider dans l’avenir mon fils qui est 1ere college. finalement merci et mes respects. driss -maroc-
Vraiment trop cool et raffiné ce cour
Merciiii
Vraiment très digeste le cour
Merciiii méthodemaths
J’ai fait un bac C en 1992 et donc, que de souvenirs!
Interessant
bonjour, pouriez vous m’aider svp.
A=xpuissance ln(lnx)/lnx
pour x>0, simplifier A
Calcule ln(A) tu vas voir apparaître quelque chose de sympathique 😉
C’est super cool. Avec ce site web, je peux resoudre mes problèmes en maths.
Super cool. Je suis super content avec vos cours
C’est excellent!
Vous êtes excellents , merci beaucoup
L’explications est simplement formidable